Contact Mechanics Model
The contact mechanics model is a specific implementation of
Model interface to handle contact between
bodies.
Theory
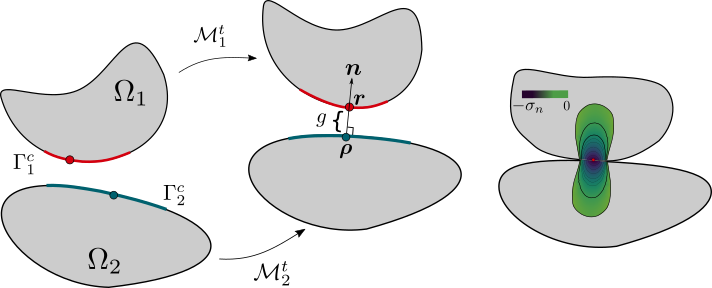
Basic notation for the contact between two bodies.
Let us consider two deformable bodies, represented as \(\Omega_\alpha\), \(\alpha=1, 2\). The boundary \(\Gamma_\alpha\) of a body is divided into three non-intersecting regions : \(\Gamma^D_\alpha\) with prescribed displacements, \(\Gamma^N_\alpha\) with prescribed tractions and \(\Gamma^C_\alpha\) where the two bodies \(\Omega_1\) can potentially come into contact such that:
The motion of the two bodies is described in a fixed spatial frame defined by orthonormal basis \([\boldsymbol{e}_x, \boldsymbol{e}_y, \boldsymbol{e}_z]\) by mapping \(\mathcal{M}_\alpha^t\) in time interval \(t \in [0, T]\). In reference configuration \(i.e.~ t=0\), the position vector for an arbitrary point on body \(\Omega_\alpha\) is represented as \(\boldsymbol{X}_\alpha\) and in actual configuration the points are denoted by small letters for example \(\boldsymbol{x}\). Fig. 24 shows the motion of two bodies from the reference to actual configuration. During the motion, the bodies can potentially come in contact along \(\Gamma^C_\alpha\) as shown in Fig. 24, termed as potential contact zone. Upon contact, two physical conditions need to be satisfied \((i)\) the two surfaces \(\Gamma^C_\alpha\) cannot interpenetrate at any time during motion \((ii)\) forces must be exerted by bodies along the \(\Gamma^C_\alpha\) to resist the interpenetration as well as relative motion along the contacting surfaces. Of the two conditions, the non-penetration of bodies can be defined by a gap function \(g\) which represents the separation between the two bodies:
where \(\boldsymbol{r} \in \mathcal{M}[\Gamma^C_1]\) is the position of point \(\boldsymbol{X}_1\) at time \(t\) , \(\boldsymbol{\rho} \in \mathcal{M}[\Gamma^C_2]\) is the closest point projection of \(\boldsymbol{r}\) and \(\boldsymbol{n}\) is the outward normal at \(\boldsymbol{\rho}\) (see Fig. 24 b). To preclude the interpenetration, the gap function is constrained with \(g \geq 0\), as it is shown in Cref{fig:body-contact}b. When the two bodies eventually come in contact, the gap vanishes \(i.e.~ g=0\) which leads to the development of tractions \(\boldsymbol{T}_\alpha\) along the contact interface. Thus, the boundary value problem can be formulated for the two bodies \(\Omega_\alpha\) with contact constraints as an extra boundary condition:
Solution spaces \(\mathcal{U}_\alpha\) and weighting spaces \(\mathcal{W}_\alpha\) are defined for each body:
The variational form for each body \(\alpha\) is given as
In equilibrium state, following Newton’s \(3^{rd}\) law, it can be stated the forces exerted by two bodies along \(\Gamma^C_\alpha\) are equal and opposite:
This allows to replace the two integrals over contact surfaces $Gamma^C_alpha$ with a single integral over any one of the surfaces:
The contact traction \(\boldsymbol{T}_1\) can be decomposed into its normal and tangential components as:
where \(\boldsymbol{T}^n\) is the component along the normal vector \(\boldsymbol{n}\) and \(\boldsymbol{T}^t\) is the component tangential to \(\boldsymbol{n}\) developed due to the friction along the surfaces. Upon contact , the normal pressure \(\sigma_n\) associated to \(\boldsymbol{T}^n\) must be compressive to preclude the interpenetration of bodies. In general, if a point is not in contact \(g > 0\), then \(\sigma_n=0\) and in contact \(\sigma_n < 0\). This leads to the non-penetration condition:
The above set of conditions care called Hertz-Signorini-Moreau or Karush-Kuhn-Tucker condition given as:
The tangential component of the contact traction is defined as :
where \(\boldsymbol{\sigma}\) is the Cauchy stress tensor and $boldsymbol{n}$ is the outward normal at \(\boldsymbol{\rho}\). The direction of tangential traction, \(\boldsymbol{s}\) is determined by the relative sliding velocity \(\boldsymbol{v}_t\) of the point \(\boldsymbol{r}\) and its projection point \(\boldsymbol{\rho}\) in contact and is given as:
According to the experimental observations of Amontons and~cite{coulomb}, in presence of friction, the interface develops a frictional strength which governs the sliding between them and thus constrains the tangential contact. In Akantu implementation, we restrict to the classical non-associated Coulomb’s friction law~citep{coulomb} which is widely used in many physical and engineering applications. The Coulomb’s friction law, as a first-order approximation, states that the frictional strength is proportional to the normal pressure:
where \(\mu\) is coefficient of friction between interfaces. If the tangential traction \(||\boldsymbol{T}^t||\) developed is below the frictional strength, the relative tangential sliding is zero \(i.e.~\boldsymbol{v}_t = 0\) :
The above equation denotes a stick state. As soon as the tangential stress reaches the frictional strength, the two surfaces start slipping relative to each other \(i.e.~\boldsymbol{v}_t > 0\). The slipping of the surfaces ensures that the tangential stress does not exceeds the frictional strength, \(||\boldsymbol{\sigma}_t|| -\mu|\sigma_n| = 0\). This definition of slip state is defined as:
Similar to Karush-Kuhn-Tucker condition for normal contact, the above conditions formulate the necessary conditions for tangential contact:
The above contact and frictional constraints are unilateral in nature i.e. they do not behave symmetrically with respect to gap function, g. This renders the balance of work as a variational inequality:
which makes it a non-linear optimization problem. The strategy employed (optimization techniques) to find the solution of variational inequality depends on the choice of numerical framework employed to solve the B.V.P.
To solve the minimization problem, FEM introduces the concept of active set strategy to overcome the problem. In active set strategy, it is assumed that at current solution step, the part of potential contact zone \(\Gamma^C_1\) that are in contact are known, \(\Gamma^{C\star}_1 \subseteq \Gamma^C_1\). This is achieved by first allowing the two bodies to interpenetrate and finding the interpenetrated part of potential contact zone which will denote the active set. Knowing the active set, transforms the optimization problem to a variational equality where constraints are imposed along the active part of contacting interface:
Thus, the resolution of contact problem in FEM requires two steps: finding the active set along the contacting interface and then imposing the contact constraints along the active set only. In the following section, we describe how to employ the contact detection strategies implemented within Akantu in order to find the active set and to compute contact forces.
Using the Contact Mechanics Model
The ContactMechanicsModel
object solves the contact problem. An instance of
the class can be created like this:
ContactMechanicsModel contact(mesh, spatial_dimension);
while an existing mesh has been used (see ref{sect:common:mesh}). To intialize the model object:
contact.initFull(_analysis_method = _explicit_lumped_mass);
The contact mechanics model contains Arrays:
gapscontains the nodal interpenetrating value \(g\) (positive for interpenetration, zero by default after initialization)
normalscontains the normal vector at the slave nodes (zero by default after initialization).
In Akantu, the possible contact between surfaces is divided into 3 categories.
Physical Surfaces - The contact occurs between two pyhsically defined boundaries/surfaces of a body.
Cohesive Surfaces - The contact occurs between fracturing surfaces created using
SolidMechanicsModelCohesive.All Surfaces - The contact can occur between physical as well as cohesive surfaces.
To select the contacting surfaces, one must define a
SurfaceSelector of one of the
above defined types.
To define contact between Physical surfaces, an instance of
PhysicalSurfaceSelector
is created where the mesh object (see ref{sect:common:mesh}) is
passed as an argument:
auto && surface_selector = std::make_shared<PhysicalSurface>(mesh);
To define contact between cohesive surfaces, an instance of
CohesiveSurfaceSelector
must be created. As the contact occurs between the cohesive facets,
therefore the mesh facet object is passed as an argument:
auto && surface_selector = std::make_shared<CohesiveSurface>(mesh.getMeshFacets());
To defind contact between physical and cohesive surfaces, an instance of
AllSurfaceSelector
must be created. As the contact occurs between the cohesive facets,
therefore the mesh facet object is passed as an argument:
auto && surface_selector = std::make_shared<AllSurface>(mesh.getMeshFacets());
Once a surface selector is created it must be assigned to the
ContactDetector class:
contact.getContactDetector().setSurfaceSelector(surface_selector);
Contact detection
The contact detection algorithm can receive a few parameters. It is possible to specify the master/slave surfaces with their string identifier. The geometrical projections are performed with iterations which can be controlled as a classical optimization problem. A typical detection configuration is given below:
contact_detector [
type = explicit
master = contact_bottom
slave = contact_top
projection_tolerance = 1e-10
max_iterations = 100
extension_tolerance = 1e-5
]
Contact resolution
The contact resolution defines the surface tractions due to contact both for normal and tangential contact. A typical configuration for a penalization formulation is as follows:
contact_resolution penalty_linear [
name = contact_top
mu = 0.0 # friction coefficient
epsilon_n = 4e5 # normal penalization
epsilon_t = 1e5 # friction penalization
is_master_deformable = false # when master is rigid => computational savings
]
Coupling with SolidMechanicsModel
To couple the
ContactMechancisModel
contact mechanics model with
SolidMechanicsModel a
dedicated coupler class CouplerSolidContact is provided.
When an instance of a coupler class is created, it automatically creates the instances of solid mechanics model and contact mechanics model. The two objects can be retrived from the coupler class.
CouplerSolidContact coupler(mesh);
auto & solid = coupler.getSolidMechanicsModel();
auto & contact = coupler.getContactMechanicsModel();
Simply initializing the coupler initializes the two models.
coupler.initFull( _analysis_method = _explicit_lumped_mass);
However to set the material selector and the contact detector for the two models, one must set them using directly the instance of the two model classes.
auto && selector = std::make_shared<MeshDataMaterialSelector<std::string>>(
"physical_names",solid);
solid.setMaterialSelector(selector);
auto && surface_selector = std::make_shared<PhysicalSurfaceSelector>(mesh);
contact.getContactDetector().setSurfaceSelector(surface_selector);
The dumping fields/vectors belonging to the solid mechanics model and contact mechanics model can directly be set through the coupler class.
coupler.setBaseName("contact-explicit-dynamic");
coupler.addDumpFieldVector("displacement");
coupler.addDumpFieldVector("normal_force");
coupler.addDumpFieldVector("external_force");
coupler.addDumpFieldVector("internal_force");
coupler.addDumpField("gaps");
coupler.addDumpField("areas");
coupler.addDumpField("stress");
Finally to solve the two models solveStep function of coupler class must be
invoked.
coupler.solveStep();
Coupling with SolidMechanicsModelCohesive
To use the contact mechanics model with cohesive elements, one must use the
CouplerSolidCohesiveContact to
coupler the ContactMechancisModel
with
SolidMechanicsModelCohesive.
The initialization and invocation of the functions are similar to
CouplerSolidContact except a few
changes.
solid = coupler.getSolidMechanicsModelCohesive();
While initializing the coupler, the nature of cohesive elements (extrinsic/intrinsic) should need to be passed.
coupler.initFull( _analysis_method = _explicit_lumped_mass, _is_extrinsic=true);
To ensure that cohesive elements break during an explicit insertion, one must
call the function checkCohesiveStress() after
solveStep().
coupler.solveStep();
solid.checkCohesiveStress();